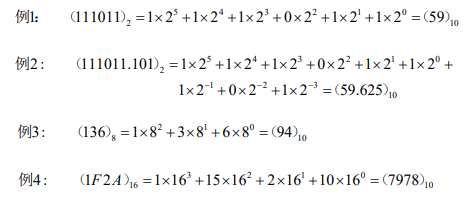2进制,8进制,16进制
2进制,8进制,16进制
2进制,8进制,16进制

数制 十进制数 二进制数 八进制数 十六进制数
数码 0~9 0~1 0~7 0~9,A~F,a~f
基 10 2 8 16
权 10º ，10¹，10²，… 2º ，2¹，2²，… 8º ，8¹，8²，… 16º ，16¹，16²，…
表示
特点 逢十进一 逢二进一 逢八进一 逢十六进一

表示: 八进制： 4275 = 4*8³ + 2*8² + 7*8¹ + 5*8º

其他转十进制

将二进制、八进制、十六进制转换为十进制

方法: 按权相加

将二进制、八进制、十六进制转换为十进制

将二进制、八进制、十六进制转换为十进制

十进制转其他

将十进制转换为二进制、八进制、十六进制

步骤：首先进行整数部分转换，然后进行小数部分转换。

(1）整数部分转换
方法：连续除以基，从低到高记录余数，直至商为0

(2）小数部分转换
方法：连续乘以基，从高到低记录整数部分，直至结果的小数部分为0

整数部分

将十进制数（29）转换成二进制数结果为( 11101 )

方法一:

进制之间转换

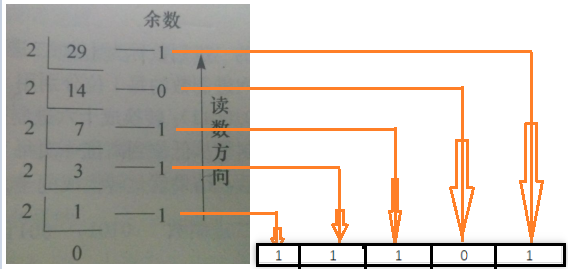
方法二:

2的次方 2^5 2^4 2^3 2^2 2^1 2^0
值 32 16 8 4 2 1
29 0 1 1 1 0 1

从左至右依次开始：比29小的取0, 比29大的取1,

demo2 小数部分

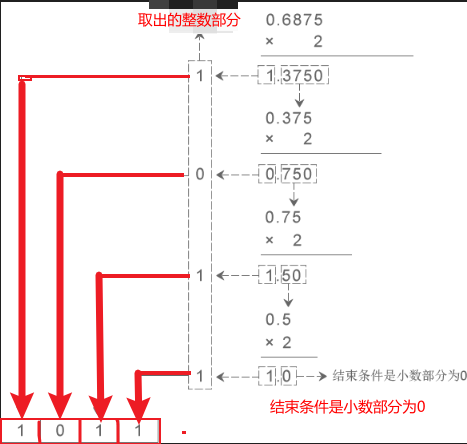
将十进制数（0.6875）转换成二进制数结果为( 0.1011 )

1
2
3
4
0.6875*2 = 1.375 ---> 取个位数1
0.375*2 = 0.75 ---> 取个位数0
0.75*2 = 1.5  ---> 取个位数1
0.5*2 = 1.0  ---> 取个位数1

进制之间转换

扩展

16进制转为2进制

1
2
3
4
5
6
7
8
9
逐位转换:只需把每一位，变成二进制的四位数，然后拼在一起

#demo
十六进制: BC.9
二 进 制: 1011 1100. 1001

#demo2
十六进制: 28AF
二 进 制: 0010 1000 1010 1111

2进制转为16进制

1
2
3
4
5
6
4位分组、按组转换

#demo
二 进 制:  11 1101
>中间过程: 0011 1101
十六进制:  3D

二进制的位运算

位运算主要包括：与(AND)、或(OR)、非(NOT)、异或(XOR)

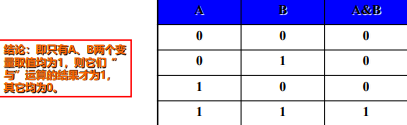
与 C语言中用 & 来表示,取值情况如下

A B A&B
0 0 0
0 1 0
1 0 0
1 1 1

与

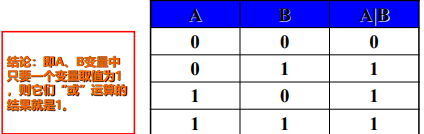
或 C语言中用 | 来表示,取值情况如下

A B A\ B
0 0 0
0 1 1
1 0 1
1 1 1

或

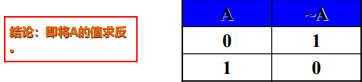
非 C语言中用 ~ 来表示,取值情况如下

A ~A
0 1
1 0

非

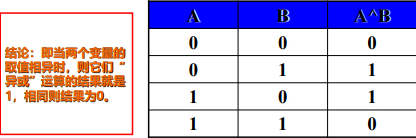
异或 C语言中用 ^ 来表示,取值情况如下

异或逻辑: 相同为0,不同为1

异或运算的特征：

  1. 任何数和 0 做异或运算，结果仍然是原来的数，即 a ⊕ 0=a。
  2. 任何数和其自身做异或运算，结果是 0，即 a ⊕ a=0。
  3. 异或运算满足交换律和结合律，即 a ⊕ b ⊕ a = b ⊕ a ⊕ a = b ⊕ (a ⊕ a)= b ⊕ 0 = b

异或（xor）是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”，计算机符号为“XOR”。其运算法则为： a⊕b = (¬a ∧ b) ∨ (a ∧¬b)

异或也叫半加运算，其运算法则相当于不带进位的二进制加法：二进制下用1表示真，0表示假，则异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1），这些法则与加法是相同的，只是不带进位，所以异或常被认作不进位加法。

A B A^B
0 0 0
0 1 1
1 0 1
1 1 0

异或

异或 运算demo

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * @param {number[]} nums
 * @return {number}
 */
var singleNumber = function(nums) {
    let single = 0;
    for (let i = 0; i < nums.length; i++) {
        single ^= nums[i];
    }
    return single;
};

// let testNums = [2, 2, 1];
// 分析:  2 ⊕ 2 ⊕ 1 =(2 ⊕ 2) ⊕ 1 = 0 ⊕ 1 = 1
// let testNums = [4,1,2,1,2];
// 分析:  4 ⊕ 1 ⊕ 2 ⊕ 1 ⊕ 2 = (1 ⊕ 1) ⊕ (2 ⊕ 2) ⊕ 4 = 0 ⊕ 0 ⊕ 4 = 3
let testNums = [1, 3, 2, 1, 2];
// 分析:  1 ⊕ 3 ⊕ 2 ⊕ 1 ⊕ 2= (1 ⊕ 1) ⊕ （2 ⊕ 2）⊕ 3= 0 ⊕ 0 ⊕ 3 = 3
let res = singleNumber(testNums)
console.log(res);