计算两点之间的距离
计算两点之间的距离

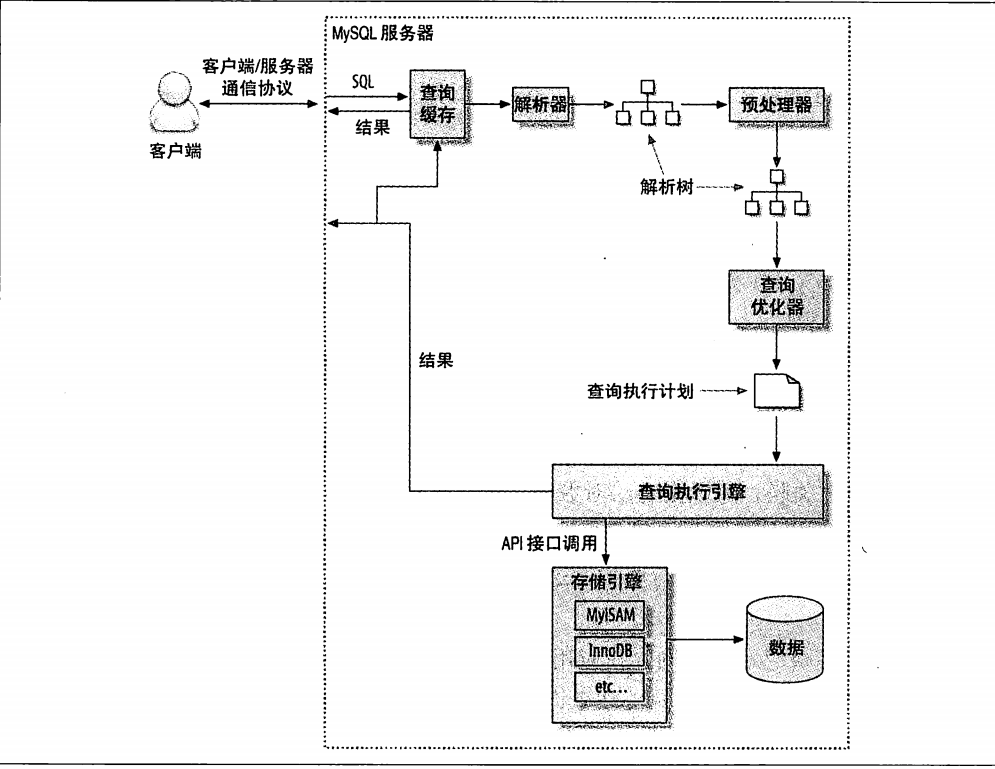
MySql查询执行流程图

1
2
3
4
5
发送语句
查询缓存
查询优化
执行查询
返回结果

mysql查询执行流程图

计算两点之间的距离

一个典型的例子是计算以某个点为中心，一定半径内的所有点。典型的实际案例可能是查找某个附近所有可以出租的房子，或者社交网站中“匹配”附近的用户，等等。假设我们有如下表：

1
2
3
4
5
6
7
8
9
CREATE TABLE `locations` (
  `id` int(11) NOT NULL AUTO_INCREMENT,
  `name` varchar(30) DEFAULT NULL,
  `lat` float NOT NULL,
  `lon` float NOT NULL,
  PRIMARY KEY (`id`)
) ENGINE=MyISAM DEFAULT CHARSET=latin1;

INSERT INTO locations(name,lat,lon)VALUES("Charlottesville,Virginia",38.03,-78.48),("Chicago,Illinois",41.85,-87.65),("Mashington,DC",38.89,-77.04)

这里经度和纬度的单位是“度”，通常我们假设地球是圆的，然后使用两点所在最大圆（半正矢）公式来计算两点之间的距离。现在有坐标latA和lonA、latB和lonB，那么点A和点B的距离计算公式如下：

1
2
3
4
AcOS(
COS(latA)*COS(latB)*COS(lonA-lonB)
+SIN(1atA)*SIN(LatB)
)

计算出的结果是一个弧度，如果要将结果的单位转换成英里或者千米，则需要乘以地球的半径，也就是3959英里或者6371千米。假设我们需要找出所有距离Baron所居住的地方Charlottesville100英里以内的点，那么我们需要将经纬度带入上面的计算公式：

1
2
3
4
5
6
7
8
9
10
11
12
13
SELECT * FROM locations 
WHERE 
3979*ACOS(
COS(radians(lat))*COS(radians(38.03))*COS(radians(lon)-radians(-78.48))+
SIN(radians(lat))*SIN(radians(38.03))
)<=100;

+----+--------------------------+-------+--------+
| id | name                     | lat   | lon    |
+----+--------------------------+-------+--------+
|  1 | Charlottesville,Virginia | 38.03 | -78.48 |
|  3 | Mashington,DC            | 38.89 | -77.04 |
+----+--------------------------+-------+--------+

这类查询不仅无法使用索引，而且还会非常消耗CPU时间，给服务器带来很大的压力，而且我们还得反复计算这个。那要怎样优化呢?这个设计中有几个地方可以微优化。第一，看看是否真的需要这么精确的计算。其实这种算法已经有很多不精确的地方了，如下所示：两个地方之间的直线距离可能是100英里，但实际上它们之间的行走距离很可能不是这个值。无论你们在哪两个地方，要到达彼此位置的行走距离多半都不是直线距离，路上可能需要绕很多的弯，比如说如果有一条河，需要绕远走到一个有桥的地方。所以，这里计算的绝对距离只是一个参考值。

如果我们根据邮政编码来确定某个人所在的地区，再根据这个地区的中心位置计算他和别人的距离，那么这本身就是一个估算。Baron 住在Charlottesville，不过不是在中心地区，他对华盛顿物理位置的中心也不感兴趣。所以，通常并不需要精确计算，很多应用如果这样计算，多半是认真过头了。这类似于有效数字的估算：计算结果的精度永远都不会比测量的值更高。（换句话说，“错进，错出”。）

如果不需要太高的精度，那么我们认为地球是圆的应该也没什么问题，其实准确的说应该是椭圆。根据毕达哥拉斯定理，做些三角函数变换，我们可以把上面的公式转换得更简单，只需要做些求和、乘积以及平方根运算，就可以得出一个点是否在另一个点多少英里之内。益习等等，为什么就到这为止？我们是否真需要计算一个圆周呢？为什么不直接使用一个正方形代替?边长为200英里的正方形，一个顶点到中心的距离大概是141英里，这和实际计算的100英里相差得并不是那么远。那我们根据正方形公式来计算弧度为0.0253（100英里）的中心到边长的距离：

1
2
3
4
5
6
7
8
9
10
SELECT * FROM locations 
WHERE lat BETWEEN 38.03 - DEGREES(0.0253) AND 38.03 + DEGREES(0.0253)
AND   lon BETWEEN -78.48 - DEGREES(0.0253) AND -78.48 + DEGREES(0.0253);

+----+--------------------------+-------+--------+
| id | name                     | lat   | lon    |
+----+--------------------------+-------+--------+
|  1 | Charlottesville,Virginia | 38.03 | -78.48 |
|  3 | Mashington,DC            | 38.89 | -77.04 |
+----+--------------------------+-------+--------+

现在我们看看如何使用索引来优化这个查询。简单地，我们可以增加索引（lat,lon)或者（lon,lat)。不过这样做效果并不会很好。正如我们所知，MySQL5.5和之前的版本，如果第一列是范围查询的话，就无法使用素引后面的列了。因为两个列都是范围的，所以这里只能使用索引的一个列（BETMEEN等效于一个大于和一个小于）。我们再次想起了通常使用的IN（）优化。我们先新增两个列，用来存储坐标的近似值FLOOR()，然后在查询中使用IN（）将所有点的整数值都放到列表中。下面是我们需要新增的列和索引：

1
2
3
4
5
6
7
8
ALTER TABLE locations ADD lat_floor INT NOT NULL DEFAULT 0, 
ADD lon_floor INT NOT NULL DEFAULT 0, 
ADD KEY (lat_floor,lon_floor);

-----------------------------------------

UPDATE locations
SET lat_floor = FLOOR(lat),lon_floor=FLOOR(lon);

现在我们可以根据坐标的一定范围的近似值来搜索了，这个近似值包括最小值和最大值，地理上分别对应的是南北。下面的查询为我们只展示了如何查某个范围的所有点：数值需要在应用程序中计算而不是MySQL中：

1
2
3
4
5
6
7
8
9
10
SELECT  FLOOR(38.03 - DEGREES(0.0253))AS lat_1b,
CEILING( 38.03 + DEGREES(0.0253))AS lat_lub,
FLOOR(-78.48 - DEGREES(0.0253))AS 1on_1b,
CEILING(-78.48 + DEGREES(0.0253))AS 1on_ub;
------------------------------------------------------
+--------+---------+--------+--------+
| lat_1b | lat_lub | 1on_1b | 1on_ub |
+--------+---------+--------+--------+
|     36 |      40 |    -80 |    -77 |
+--------+---------+--------+--------+

现在我们就可以生成IN（）列表中的整数了，也就是前面计算的地板和天花板数值之间的数字。下面是加上WHERE条件的完整查询：

1
2
3
4
5
6
7
8
9
10
11
12
13
现在我们就可以生成IN（）列表中的整数了，也就是前面计算的地板和天花板数值之间的数字。下面是加上WHERE条件的完整查询：

SELECT * FROM locations
WHERE lat BETWEEN 38.03-DEGREES(0.0253)AND 38.03 + DEGREES(0.0253)
AND lon BETWEEN-78.48-DEGREES(0.0253)AND-78.48 +DEGREES(0.0253)
AND lat_floor IN(36,37,38,39,40)AND lon_floor IN(-80,-79,-78,-77);

+----+--------------------------+-------+--------+-----------+-----------+
| id | name                     | lat   | lon    | lat_floor | lon_floor |
+----+--------------------------+-------+--------+-----------+-----------+
|  1 | Charlottesville,Virginia | 38.03 | -78.48 |        38 |       -79 |
|  3 | Mashington,DC            | 38.89 | -77.04 |        38 |       -78 |
+----+--------------------------+-------+--------+-----------+-----------+

使用近似值会让我们的计算结果有些偏差，所以我们还需要一些额外的条件剔除在正方形之外的点。这和前面使用CRC32做哈希索引类似：先建一个索引帮我们过滤出近似值，再使用精确条件匹配所有的记录并移除不满足条件的记录。事实上，到这时我们就无须根据正方形的近似来过滤数据了，我们可以使用最大圆公式或者毕达哥拉斯定理来计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
SELECT * FROM locations
WHERE lat_floor IN(36,37,38,39,40)
AND lon_floor IN(-80,-79,-78,-77)
AND 3979*ACOS(
COS(radians(lat))*COS(radians(38.03))*COS(radians(lon)-radians(-78.48))+SIN(radians(lat))*SIN(radians(38.03))
)<=100;

----------------------------------------------

+----+--------------------------+-------+--------+-----------+-----------+
| id | name                     | lat   | lon    | lat_floor | lon_floor |
+----+--------------------------+-------+--------+-----------+-----------+
|  1 | Charlottesville,Virginia | 38.03 | -78.48 |        38 |       -79 |
|  3 | Mashington,DC            | 38.89 | -77.04 |        38 |       -78 |
+----+--------------------------+-------+--------+-----------+-----------+

这时计算精度再次回到前面——使用一个精确的圆周——不过，现在的做法更快。只要能够高效地过滤掉大部分的点，例如使用近似整数和索引，之后再做精确数学计算的代价并不大。只是不要直接使用大圆周的算法，否则速度会很慢。

Sphinx有很多内置的地理信息搜索功能，比MySQL实现要好很多。如果正在考虑使用MyISAM的GIS函数，并使用上面的技巧来计算，那么你需要记住：这样做效果并不会很好，MyISAM本身也并不适合大数据量、高并发的应用，另外MyISAM本身还有一些弱点，如数据文件崩溃、表级锁等。

回顾一下上面的案例，我们采用了下面这些常用的优化策略：

·尽量少做事，可能的话尽量不做事。这个案例中就不要对所有的点计算大圆周公式；先使用简单的方案过滤大多数数据，然后再到过滤出来的更小的集合上使用复杂的公式运算。

快速地完成事情。确保在你的设计中尽可能地让查询都用上合适的索引，使用近似计算（例如本案例中，认为地球是平的，使用一个正方形来近似圆周）来避免复杂的计算。

需要的时候，尽可能让应用程序完成一些计算。例如本案例中，在应用程序中计算所有的三角函数。